|
Cryptography is necessary to the functioning of modern society, yet the design of symmetric-key ciphers is with some justification considered a Black Art. Certainly the ``blackest" part of such design is the construction of the nonlinear substitution (or S-box) function that provides the bulk of a cipher's resistance against attack. Up until very recently, these functions were designed primarily as random lookup tables and tested against known attacks. This is hardly ideal. However, a new method of designing S-boxes has been advanced that
represents cipher components as functions on finite fields of the
form This stuff is not just of theoretic interest- the cipher Rijndael was developed using this process, and in 2000 was chosen from a field of very qualified candidates to be the Advanced Encryption Standard by NIST, in large part due to its clean, mathematically-derived design. Mathematics trumps black magic. |
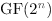 . Using a wide array of tools suitable security
criteria can be defined, and several categories of functions can be
proven to satisfy the criteria to maximal or near-maximal extents.
Among the tools are the field trace
. Using a wide array of tools suitable security
criteria can be defined, and several categories of functions can be
proven to satisfy the criteria to maximal or near-maximal extents.
Among the tools are the field trace 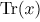 and Walsh transform
and Walsh transform
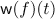 . Representing the criteria will be measures of
nonlinearity
. Representing the criteria will be measures of
nonlinearity 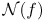 , and the concept of a function being
differentially
, and the concept of a function being
differentially  -uniform, which tracks correlation between
input and output differences. Finally, functions of the form
-uniform, which tracks correlation between
input and output differences. Finally, functions of the form
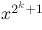 and
and 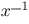 will be paid special attention.
will be paid special attention.